Types of Price Elasticity of Demand | Free Economic Blogs

Types of Price Elasticity of Demand

Price Elasticity of Demand

According to Prof. Alfred Marshall, price elasticity of demand is a ratio of proportionate change in the quantity demanded of a commodity to a given proportionate change in its price.

Ed = Percentage change in Quantity Demanded / Percentage change in Price

Symbolically,
Ed = %∆Q / %∆P ,
Ed = ∆Q/Q ÷ ∆P/P
Ed = ∆Q/Q × P/∆P
Where,
Q = Original quantity demanded
∆Q = Difference between the new quantity and original quantity demanded
P = Original price
∆P = Difference between new price and original price

Following are the types of Price Elasticity of Demand:

1) Perfectly Elastic Demand (Ed = ∞) :
When a slight or zero change in the price brings about an infinite change in the quantity demanded of that commodity, it is called perfectly elastic demand. It is only a theoretical concept. For example, a 10% fall in price may lead to an infinite rise in demand.

Ed = Percentage change in Quantity Demanded / Percentage change in Price = ∞
Ed = ∞

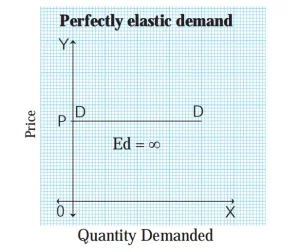
In the above figure, the demand curve DD is a horizontal line parallel to the X-axis indicating perfectly elastic demand.

2) Perfectly inelastic demand (Ed = 0) :
When a percentage change in price has no effect on the quantity demanded of a commodity it is called perfectly inelastic demand. For example, a 20% fall in price will have no effect on the quantity demanded.

Ed = %∆Q / %∆P
Ed = 0/20 = 0
Ed = 0
In practice, such a situation rarely occurs. For example, demand for salt, and milk.

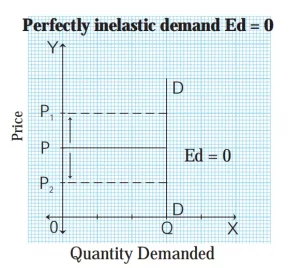
In the above figure, when price rises from OP to OP₁ or when the price falls from OP to OP₂, demand remains unchanged at OQ. Therefore, the demand curve is a vertical straight line parallel to the Y axis, indicating perfectly inelastic demand.

3) Unitary elastic demand (Ed = 1) :
When a percentage change in price leads to a proportionate change in quantity demanded then demand is said to be unitary elastic. For example, 50% fall in price of a commodity leads to 50% rise in quantity demanded.

Ed = %∆Q / %∆P
Ed = 50/50 = 1
∴ Ed = 1

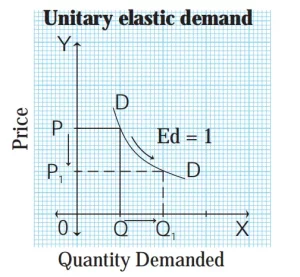
In the above figure, when price falls from OP to OP₁ (50%), demand rises from OQ to OQ₁ (50%). Therefore, the slope of the demand curve is a ‘rectangular hyperbola’.

4) Relatively elastic demand (Ed >1) :
When a percentage change in price leads to more than proportionate change in quantity demanded, the demand is said to be relatively elastic. For example, 50% fall in price leads to 100% rise in quantity demanded.

Ed = %Q / %P
Ed = 100/50
∴Ed = 2
Ed > 1

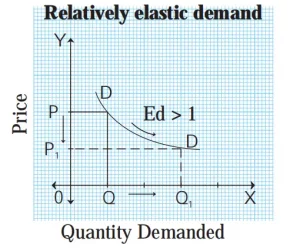
In the above figure, when price falls from OP to OP₁ (50%), demand rises from OQ to OQ₁ (100%). Therefore, the demand curve has a flatter slope.

5) Relatively inelastic demand (Ed < 1) :
When a percentage change in price leads to less than proportionate change in the quantity demanded, demand is said to be relatively inelastic. For example, 50% fall in price leads to 25% rise in quantity demanded.

Ed = %∆Q / %∆P = 25/50 = 0.5
Ed = 0.5
∴Ed < 1

In the above figure, when price falls from OP to OP₁ (50%), demand rises from OQ to OQ₁ (25%). Therefore, the demand curve has a steeper slop

• Microeconomic Definition | Historical Review of Microeconomics
• Scope Or Nature of Microeconomics
• Features of Microeconomics
• Importance of Microeconomics
• Importance of Law of Diminishing Marginal Utility
• Utility in Economics ( Concepts of Utility )
• Features of Utility
• Types of Utility